Mi problema

El problema consiste en encontrar un "anagrama" es decir en componer una sola palabra con las lñetras contenidas en la siguiente n palabra.

HACER DAS NITIDO

¿Cual es la incognita ?

una palabra

¿Cuales son los datos ?

Las 3 palabras establecidas anteriormente

Pasos :

1.-La palabra que se desea obtener tiene 14 letras

2.- Podemos realizar el problema atra vez de una figura

3.- Sabemos que dicha palabra consta de 6 silabas.- Lo primero que debenos hacer es ordenar las vocales y las consonantes que forman dicha palabra , la cual es de la siguiente manera

AAEIIO CDD
La palabra encontrada es la siguiente:


AERODINAMISTAD

CONCLUSIONES:

UN SOLO COMENTARIO LO DICE TODO:

Antes que nada no cave duda que la inteligencia se adquiere atra vez de la perseverancia y el estudio constante que hacen los grandes y buenos maestros y que puedo decir profesor que usted es uno de esos profesores que le gusta innovar y quiere que nosotros como alumnos seamos o mas que nada aprendamos cosas nuevas no las cosas que se enseñan cotidianamente.

De manera particular en este curso que usted nos impartio a mi me sirvio de gran ayuda para poder hacer buen uso del internet, con usted aprendimos a como hacer en publico atravez del internet nuestras tareas y ejercicios que usted dejaba y asi usted poder revisar y dar sugerencias de como debemos plantear un problema, y que tecnicas que debemos implementar para poder desarrollarlo y tener buenos resultados .
Con la ayuda del libro de polya me di cuenta que hay diversas formas de avordar un problema y de poder resolverlo por lo que dice usted que hay que ser original para poder desarrollar a nuestra manera los problemas y darle solucion a nuestra conveniencia...

No tengo mas palabras para poder agradeserle a los maestros y en especial a usted profesor Eduardo Cantoral por avernos ayudado a como ir desarrollandonos como unos buenos estudiantes y no ser del monton como otros si no ser uno de los primeros ....


Es mi primer año en mi carrera y me siento onrado por a ver compartido buenos y malos momentos quizas con mis compañeros solo espero que no y que sigamos todos adelante ....

"QUE DIOS LOS VENDIGA A TODOS Y CADA UNO DE NOSOTROS Y QUE ESTE PRIMER SEMESTRE NOS SIRVA DE REFLEXION EL CUAL PARA MI NO FUE NADA FACIL PERO GRACIAS ADIOS YA VOY SALIENDO"

"Las Derivadas en las Matematicas"

El conjunto de todas las funciones presenta una diversidad tal que es casi imposible descubrir propiedades generales interesantes que convengan a todas ellas. Puesto que las funciones continuas constituyen una clase restringida, cabría esperar que se hallaran algunos teoremas no triviales para ellas... Pero los resultados más interesantes y más penetrantes acerca de funciones sólo se obtendrán cuando limitemos aún más nuestra atención a funciones que tienen mayor derecho aún a recibir el nombre de 'razonables', con un comportamiento aún más regular que la mayor parte de las funciones continuas. (Spivak, 181-2).
El incremento Dx de una variable x es el aumento o disminución que experimenta, desde un valor x = x₀ a otro x = x₁ de su campo de variación. Así, pues,

o bien

Si se da un incremento Dx a la variable x, (es decir, si x pasa de x = x₀ a x = x₀ + Dx), la función y = f (x) se verá incrementada en Dy = f (x₀ + Dx) - f (x₀) a partir del valor y = f (x₀). El cociente

recibe el nombre de cociente medio de incrementos de la función en el intervalo comprendido entre x = x₀ a x = x₀ + Dx. (Ayres, 22)].

Pendiente

[Si h ¹ 0, entonces los dos puntos distintos (a, f (a)) y (a+h, f (a+h)) determinan, como en la figura 6, una recta cuya pendiente es

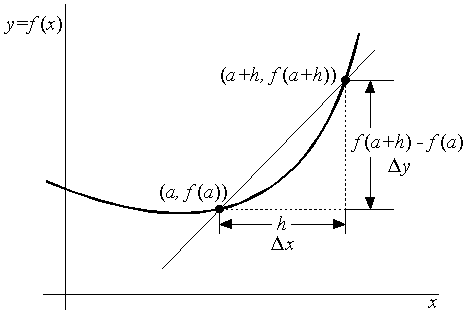
Figura 6.

Como indica la figura 7, la 'tangente' en (a, f (a)) parece ser el límite, en algún sentido, de estas 'secantes', cuando h se aproxima a 0. Hasta aquí no hemos hablado nunca del 'límite' de rectas, pero podemos hablar del límite de sus pendientes: La pendiente de la tangente (a, f (a)) debería ser

"La Espiral de Ulam"

La espiral de Ulam, descrita por el matemático polacoestadounidense Stanisław Marcin Ulam (1909-1984), es una forma de representación gráfica de números primos que muestra un patrón.

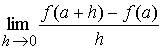
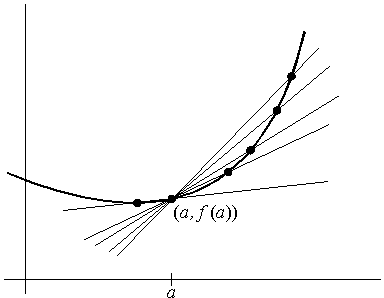
En 1963, Ulam, aburrido durante una conferencia científica, estaba haciendo garabatos en una hoja de papel. Dispuso una malla de números en espiral, empezando por el 1 en el centro, el 2 a su derecha, el 3 arriba, el 4 encima del 1, el 5 a la izquierda, y así sucesivamente. Posteriormente, marcó los números primos y descubrió que los números marcados tendían a alinearse a lo largo de líneas diagonales.

Todos los números primos, excepto el 2, son impares. Como en la espiral de Ulam algunas diagonales contienen números impares y otras contienen números pares, no sorprende ver cómo los números primos caen todos (salvo el 2) en diagonales alternas. Sin embargo, entre las diagonales que contienen números impares, unas contienen una proporción visiblemente mayor que otras de números primos.

Las pruebas que se han hecho hasta ahora confirman que, incluso si se extiende mucho la espiral, se siguen mostrando esas diagonales. El patrón se muestra igualmente aunque el número central no sea 1 (en efecto, puede ser mucho mayor que 1). Esto significa que hay muchas constantes enteras b y c tales que la función

f(n) = 4n² + bn + c

genera, a medida que crece n a lo largo de los naturales {1, 2, 3, ...}, una gran cantidad de números primos en comparación con la proporción de primos existente en números de magnitud similar. Este hallazgo fue tan célebre que la espiral de Ulam apareció en la cubierta de la revista Scientific American en marzo de 1964.

A una distancia suficiente del centro, también se aprecian claramente líneas horizontales y verticales.

Existen otras variantes de la espiral de Ulam, tales como la espiral de Sacks ue también muestran patrones sin explicación aparente.

"El origen del Cero"

Las cuentas de la babilonios comenzaron a utilizar una señal para indicar cuando las casas estaban vacías
unos 300 años antes de Cristo. Sí, aunque los egipcios no tenían conocimiento de cero.
Todo el trabajo increíble de la geometría y las matemáticas utilizadas en las pirámides y el Delta del Nilo no tenía cero. La aceptación de una cosa abstracta tomó tiempo y los obstáculos que enfrentan inconmensurable.
La Iglesia Católica protegidas del pensamiento aristotélico, cuando no era un elemento
no agresivo, que no significaba nada, o peor, el vacío, como el número cero.
El calendario, por ejemplo, tuvo varios fracasos por la falta de cero.
Pero el cero no sólo cambió los principios matemáticos y físicos. También influyó en el arte para siempre.
Es gracias al punto cero de fuga, lo que da un sentido de la perspectiva de las pinturas, se ha creado.
Antes del siglo 15, las pinturas no tenían la vida o la profundidad. Fue el italiano Filippo Brunelleschi, que utilizó el cero para crear la sensación de espacio y dimensión. Zero es tan importante en la sociedad de hoy que toda la tecnología informática está basada en dos números: 1 (uno) y 0 (cero), que forman el sistema binario.

"Quipus del Tahuantinsuyo" es el título de la obra en la que el autor analiza lo que él mismo califica como "calculadora" inca, un modo de sumar, restar, multiplicar y dividir con pequeñas piedras. Ell investigador espera dar un paso más en el proceso para descifrar los quipus, tejidos con nudos que servían como "libros de contabilidad" pero también posiblemente para registrar textos.

Para resolver el misterio alrededor del sistema de cálculo inca o yupana, el peruano Andrés Chirinos sólo necesitó un dibujo del cronista Huamán Poma de Ayala y la mítica capacidad de los antiguos peruanos para el cómputo.

"Quipus del Tahuantinsuyo" es el título de la obra, presentada el martes y en la que Chirinos analiza lo que él mismo califica como "calculadora" inca, un modo de sumar, restar, multiplicar y dividir con pequeñas piedras

Con este trabajo el investigador espera dar un paso más en el proceso para descifrar los quipus, tejidos con nudos que servían como "libros de contabilidad" pero también posiblemente para registrar textos.

"Era un acertijo", declaró a Efe éste antropólogo peruano al recordar el proceso que le llevó, en base al dibujo de Poma de Ayala e ideas de la cultura indígena como "la simetría o los paralelismos", a elaborar su novedosa teoría.

"Encontré algunos valores que funcionaban, y me entusiasmó, pero no llegué a imaginarme lo que podía ser", agregó.

Y es que aunque el sistema que ideó fue fruto de muchas horas frente a la tabla de madera de once agujeros que fabricó copiando el dibujo del cronista, el desarrollo y perfeccionamiento de su teoría se logró gracias a la aplicación práctica de la misma.

"Descripcion del cuerpo de Gabriel"

El Cuerno de Gabriel o Trompeta de Torricelli es una figura geométrica ideada por Evangelista Torricelli que tiene la característica de poseer una superficie infinita pero un volumen finito.

Historia

En el momento de su descubrimiento, fue considerado una paradoja. Esta paradoja aparente ha sido descrita de modo informal señalando que sería necesaria una cantidad infinita de pintura para cubrir la superficie interior, mientras que sería posible rellenar toda la figura con una cantidad finita de pintura y así cubrir esa superficie.

La solución de la paradoja es que un área infinita requiere una cantidad infinita de pintura si la capa de pintura tiene un grosor constante. Esto no se cumple en el interior del cuerno, ya que la mayor parte de la longitud de la figura no es accesible a la pintura, especialmente cuando su diámetro es menor que el de una molécula de pintura. Si se considera una pintura sin grosor, sería necesaria una cantidad infinita de tiempo para que ésta llegase hasta el «final» del cuerno.

En otras palabras, llegaría un momento en el que el espesor de la trompeta sería más pequeño que una molécula de pintura con lo que, digamos, una gota de pintura cubriría el resto de la superficie de la trompeta (aunque fuera infinito). Así, que la superficie de la trompeta sea infinita no implicaría que la cantidad de pintura tenga que ser infinita.

Pero la paradoja también tiene solución incluso si suponemos una materia divisible indefinidamente (o sea, si no existen los átomos). Si el grosor de la capa de pintura es variable y disminuye indefinidamente (tendiendo a cero), la cantidad de pintura se calcularía por una integral impropia que podría ser convergente. En este caso, el espesor de la capa de pintura forzosamente debería ser igual o menor al valor de y, lo que hace que la integral impropia, en este caso, sea convergente, es decir, se necesita una cantidad finita de pintura.